The metafor Package

Raudenbush and Bryk (1985) describe the meta-analytic random- and mixed-effects models and describe restricted maximum likelihood estimation for the amount of (residual) heterogeneity (p. 80-82).¹⁾ The models and methods are illustrated with a meta-analytic dataset of studies examining how teachers' expectations about their pupils can influence actual IQ levels (Raudenbush, 1984). The data are provided in Table 1 of the article and can be loaded with:

library(metafor)
dat <- dat.raudenbush1985
dat

(I copy the dataset into dat, which is a bit shorter and therefore easier to type further below). The contents of the dataset are:

   study               author year weeks setting tester n1i n2i      yi     vi
1      1     Rosenthal et al. 1974     2   group  aware  77 339  0.0300 0.0156
2      2          Conn et al. 1968    21   group  aware  60 198  0.1200 0.0216
3      3          Jose & Cody 1971    19   group  aware  72  72 -0.1400 0.0279
4      4   Pellegrini & Hicks 1972     0   group  aware  11  22  1.1800 0.1391
5      5   Pellegrini & Hicks 1972     0   group  blind  11  22  0.2600 0.1362
6      6    Evans & Rosenthal 1969     3   group  aware 129 348 -0.0600 0.0106
7      7       Fielder et al. 1971    17   group  blind 110 636 -0.0200 0.0106
8      8             Claiborn 1969    24   group  aware  26  99 -0.3200 0.0484
9      9               Kester 1969     0   group  aware  75  74  0.2700 0.0269
10    10              Maxwell 1970     1   indiv  blind  32  32  0.8000 0.0630
11    11               Carter 1970     0   group  blind  22  22  0.5400 0.0912
12    12              Flowers 1966     0   group  blind  43  38  0.1800 0.0497
13    13              Keshock 1970     1   indiv  blind  24  24 -0.0200 0.0835
14    14            Henrikson 1970     2   indiv  blind  19  32  0.2300 0.0841
15    15                 Fine 1972    17   group  aware  80  79 -0.1800 0.0253
16    16              Grieger 1970     5   group  blind  72  72 -0.0600 0.0279
17    17 Rosenthal & Jacobson 1968     1   group  aware  65 255  0.3000 0.0193
18    18   Fleming & Anttonen 1971     2   group  blind 233 224  0.0700 0.0088
19    19             Ginsburg 1970     7   group  aware  65  67 -0.0700 0.0303

Note that the dataset includes the sampling variances (these are just the square of the standard errors reported by Raudenbush & Bryk, 1985).

The results from the random-effects model can now be obtained with:

res <- rma(yi, vi, data=dat, digits=3)
res

Random-Effects Model (k = 19; tau^2 estimator: REML)
 
tau^2 (estimated amount of total heterogeneity): 0.019 (SE = 0.016)
tau (square root of estimated tau^2 value):      0.137
I^2 (total heterogeneity / total variability):   41.86%
H^2 (total variability / sampling variability):  1.72
 
Test for Heterogeneity:
Q(df = 18) = 35.830, p-val = 0.007
 
Model Results:
 
estimate     se   zval   pval   ci.lb  ci.ub
   0.084  0.052  1.621  0.105  -0.018  0.185
 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

REML estimation is the default for the rma() function, so these results reproduce what is reported in the article. In particular, $\hat{\tau}^2 = .019$ (p. 83), $Q(df=18) = 35.83$ (p. 85), $\hat{\mu} = .084$ (p. 85), and $z = 1.62$ (p. 86) for the test $\mbox{H}_0{:}\; \mu = 0$.

The empirical Bayes estimates can be obtained with:

blup(res)

     pred    se  pi.lb pi.ub
1   0.054 0.095 -0.132 0.241
2   0.101 0.104 -0.103 0.304
3  -0.006 0.110 -0.223 0.210
4   0.214 0.137 -0.053 0.482
5   0.105 0.136 -0.162 0.372
6  -0.008 0.084 -0.174 0.157
7   0.017 0.084 -0.148 0.183
8  -0.029 0.122 -0.269 0.210
9   0.160 0.110 -0.054 0.375
10  0.249 0.127  0.000 0.497
11  0.162 0.132 -0.097 0.421
12  0.110 0.123 -0.130 0.351
13  0.065 0.131 -0.192 0.321
14  0.110 0.131 -0.146 0.367
15 -0.029 0.108 -0.241 0.183
16  0.026 0.110 -0.191 0.242
17  0.191 0.101 -0.008 0.389
18  0.074 0.079 -0.081 0.230
19  0.025 0.112 -0.195 0.245

These values are shown in the article in Figure 2.

Next, Raudenbush and Bryk (1985) use a mixed-effects model with the number of prior contact weeks as predictor/moderator. For this analysis, they recode all week values greater than 3 to 3:

dat$weeks.c <- ifelse(dat$weeks > 3, 3, dat$weeks)

Then, the mixed-effects model can be fitted with:

res <- rma(yi, vi, mods = ~ weeks.c, data=dat, digits=3)
res

Mixed-Effects Model (k = 19; tau^2 estimator: REML)
 
tau^2 (estimated amount of residual heterogeneity):     0.000 (SE = 0.007)
tau (square root of estimated tau^2 value):             0.001
I^2 (residual heterogeneity / unaccounted variability): 0.00%
H^2 (unaccounted variability / sampling variability):   1.00
R^2 (amount of heterogeneity accounted for):            100.00%
 
Test for Residual Heterogeneity:
QE(df = 17) = 16.571, p-val = 0.484
 
Test of Moderators (coefficient 2):
QM(df = 1) = 19.258, p-val < .001
 
Model Results:
 
         estimate     se    zval   pval   ci.lb   ci.ub
intrcpt     0.407  0.087   4.678  <.001   0.237   0.578  ***
weeks.c    -0.157  0.036  -4.388  <.001  -0.227  -0.087  ***
 
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

These results again match the findings from Raudenbush and Bryk (1985). The residual amount of heterogeneity is now $\hat{\tau}^2 \approx 0$ (p. 90) and the test statistic for $\mbox{H}_0{:}\; \tau^2 = 0$ is $Q_E(df=17) = 16.57$ (p. 90). The estimated model is $E(d_i) = .407 - 0.157 x_i$, where $x_i$ is the number of prior contact weeks (p. 90). The standard errors of the model coefficients are $SE[b_0] = .087$ and $SE[b_1] = .036$, so that the test statistics are $z_0 = 4.68$ and $z_1 = -4.39$, respectively (p. 92).

The empirical Bayes estimates can again be obtained with:

blup(res)

     pred    se  pi.lb pi.ub
1   0.093 0.037  0.020 0.166
2  -0.065 0.046 -0.155 0.026
3  -0.065 0.046 -0.155 0.026
4   0.407 0.087  0.237 0.578
5   0.407 0.087  0.237 0.578
6  -0.065 0.046 -0.155 0.026
7  -0.065 0.046 -0.155 0.026
8  -0.065 0.046 -0.155 0.026
9   0.407 0.087  0.237 0.578
10  0.250 0.057  0.139 0.361
11  0.407 0.087  0.237 0.578
12  0.407 0.087  0.237 0.578
13  0.250 0.057  0.139 0.361
14  0.093 0.037  0.020 0.166
15 -0.065 0.046 -0.155 0.026
16 -0.065 0.046 -0.155 0.026
17  0.250 0.057  0.139 0.361
18  0.093 0.037  0.020 0.166
19 -0.065 0.046 -0.155 0.026

which are actually the same now as the fitted values (since $\hat{\tau}^2 \approx 0$).²⁾

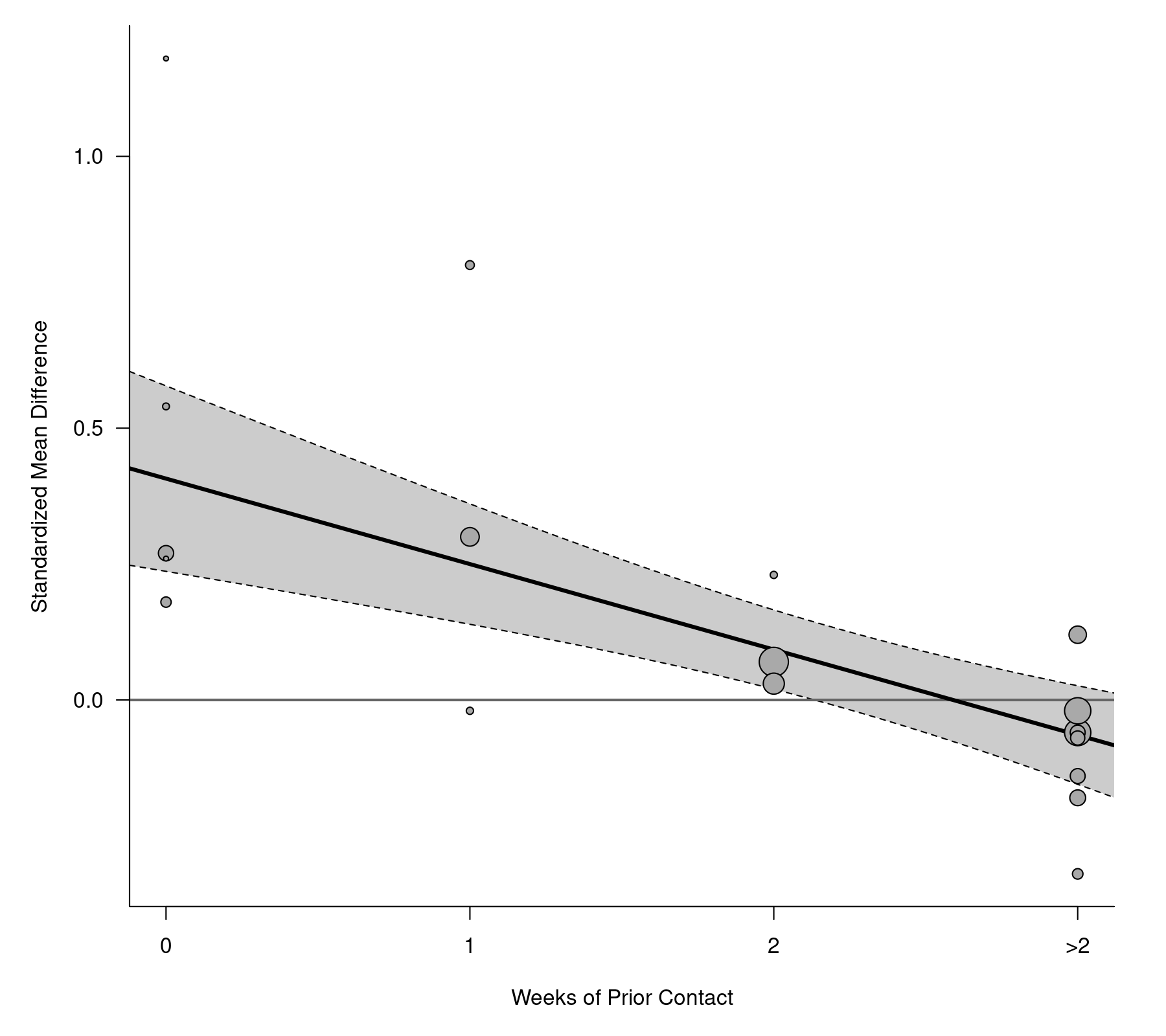
Finally, we can draw a scatterplot of the observed standardized mean differences as a function of the weeks variable (with the radius of the points drawn proportional to the inverse standard errors and hence the area of the points drawn proportional to the inverse sampling variances) with:

regplot(res, xlab="Weeks of Prior Contact", bty="l", las=1, digits=1, refline=0, xaxt="n")
axis(side=1, at=c(0,1,2,3), labels=c("0", "1", "2", ">2"))

The predicted (average) effect as a function of the weeks of prior contact (with 95% CI bounds) is also added to the plot. The resulting plot is shown below.

Raudenbush, S. W. (1984). Magnitude of teacher expectancy effects on pupil IQ as a function of the credibility of expectancy induction: A synthesis of findings from 18 experiments. Journal of Educational Psychology, 76(1), 85–97.

Raudenbush, S. W., & Bryk, A. S. (1985). Empirical Bayes meta-analysis. Journal of Educational Statistics, 10(2), 75–98.