Forest Plot with Exact Confidence Intervals
A forest plot is a commonly used visualization technique in meta-analyses, showing the results of the individual studies (i.e., the estimated effects or observed outcomes) together with their (usually 95%) confidence intervals (CIs). A four-sided polygon, sometimes called a summary 'diamond', is added to the bottom of the plot, showing the summary estimate based on the model (with the center of the polygon corresponding to the estimate and the left/right edges indicating the confidence interval limits).
Let's create such a figure for our beloved BCG vaccine dataset. First, we compute the log odds ratios and corresponding sampling variances for the studies with:
dat <- dat.bcg dat <- escalc(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat, slab=paste(author, year, sep=", ")) dat
trial author year tpos tneg cpos cneg ablat alloc yi vi 1 1 Aronson 1948 4 119 11 128 44 random -0.9387 0.3571 2 2 Ferguson & Simes 1949 6 300 29 274 55 random -1.6662 0.2081 3 3 Rosenthal et al 1960 3 228 11 209 42 random -1.3863 0.4334 4 4 Hart & Sutherland 1977 62 13536 248 12619 52 random -1.4564 0.0203 5 5 Frimodt-Moller et al 1973 33 5036 47 5761 13 alternate -0.2191 0.0520 6 6 Stein & Aronson 1953 180 1361 372 1079 44 alternate -0.9581 0.0099 7 7 Vandiviere et al 1973 8 2537 10 619 19 random -1.6338 0.2270 8 8 TPT Madras 1980 505 87886 499 87892 13 random 0.0120 0.0040 9 9 Coetzee & Berjak 1968 29 7470 45 7232 27 random -0.4717 0.0570 10 10 Rosenthal et al 1961 17 1699 65 1600 42 systematic -1.4012 0.0754 11 11 Comstock et al 1974 186 50448 141 27197 18 systematic -0.3408 0.0125 12 12 Comstock & Webster 1969 5 2493 3 2338 33 systematic 0.4466 0.5342 13 13 Comstock et al 1976 27 16886 29 17825 33 systematic -0.0173 0.0716
Next, we fit a standard random-effects model to these data with:
res <- rma(yi, vi, data=dat) res
Random-Effects Model (k = 13; tau^2 estimator: REML) tau^2 (estimated amount of total heterogeneity): 0.3378 (SE = 0.1784) tau (square root of estimated tau^2 value): 0.5812 I^2 (total heterogeneity / total variability): 92.07% H^2 (total variability / sampling variability): 12.61 Test for Heterogeneity: Q(df = 12) = 163.1649, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -0.7452 0.1860 -4.0057 <.0001 -1.1098 -0.3806 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Then we can create the forest plot with:
forest(res, header=TRUE, atransf=exp, xlim=c(-8,6), at=log(c(0.05, 0.25, 1, 4, 16)), psize=1)
The estimated log odds ratios of the individual studies and the pooled estimate of the random-effects model are back-transformed using exponentiation for easier interpretation (to be precise, atransf=exp does an axis transformation which results in a log scale for the x-axis and symmetric looking CIs).
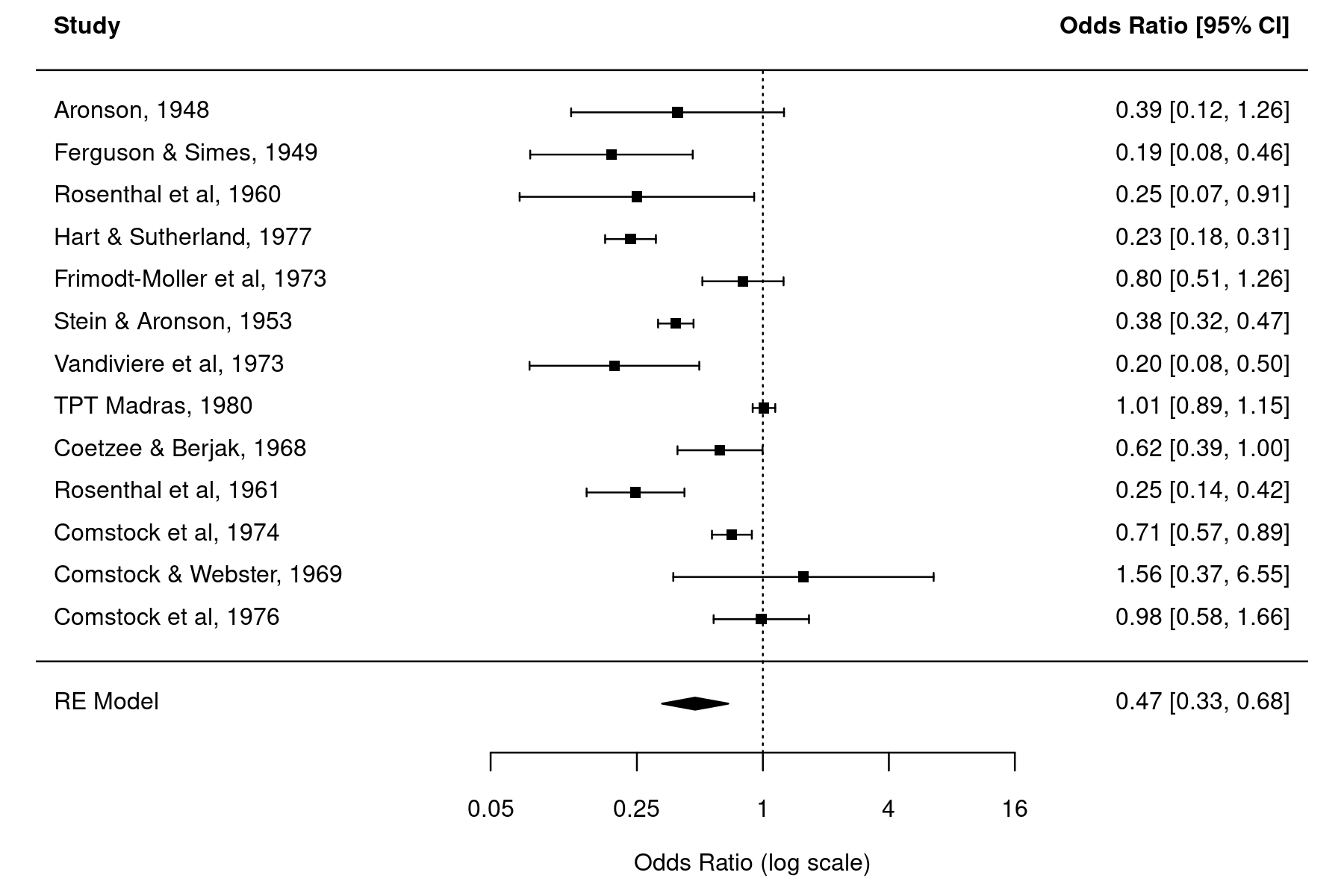
The CIs of the individual studies are so-called Wald-type confidence intervals, which are computed with $y_i \pm 1.96 \sqrt{v_i}$, where $y_i$ are the observed log odds ratios and $v_i$ the corresponding sampling variances, which are then back-transformed via exponentiation. We can also obtain these CIs as follows:
summary(dat, transf=exp)[c("yi", "ci.lb", "ci.ub")]
yi ci.lb ci.ub 1 0.3911 0.1212 1.2619 2 0.1890 0.0773 0.4621 3 0.2500 0.0688 0.9085 4 0.2331 0.1763 0.3082 5 0.8032 0.5138 1.2556 6 0.3836 0.3156 0.4662 7 0.1952 0.0767 0.4966 8 1.0121 0.8940 1.1458 9 0.6239 0.3908 0.9961 10 0.2463 0.1438 0.4219 11 0.7112 0.5711 0.8856 12 1.5630 0.3731 6.5476 13 0.9828 0.5816 1.6607
However, Wald-type CIs are approximate CIs that may not actually have the chosen coverage probability (i.e., they may cover the true outcomes more or less often than 95% of the times). For many outcome measures, we can compute 'exact' confidence intervals that are guaranteed to have the desired coverage probability (or a coverage probability that is at least as large as the chosen confidence level).
Using the same principle underlying Fisher's exact test (which makes use of the hypergeometric distribution), one can also compute exact CIs for the odds ratios in the individual 2x2 tables (which requires the use of the non-central hypergeometric distribution) as follows:
tmp <- lapply(split(dat, dat$trial), FUN = function(x) fisher.test(matrix(c(x[["tpos"]], x[["tneg"]], x[["cpos"]], x[["cneg"]]), nrow=2, ncol=2, byrow=TRUE))$conf.int) tmp <- do.call(rbind, tmp) colnames(tmp) <- c("ci.lb", "ci.ub") dat <- cbind(dat, tmp) dfround(dat[c(1:3, 10:13)], digits=c(rep(0,3),rep(4,4)))
trial author year yi vi ci.lb ci.ub 1 1 Aronson 1948 -0.9387 0.3571 0.0887 1.3703 2 2 Ferguson & Simes 1949 -1.6662 0.2081 0.0633 0.4736 3 3 Rosenthal et al 1960 -1.3863 0.4334 0.0443 0.9666 4 4 Hart & Sutherland 1977 -1.4564 0.0203 0.1733 0.3094 5 5 Frimodt-Moller et al 1973 -0.2191 0.0520 0.4977 1.2827 6 6 Stein & Aronson 1953 -0.9581 0.0099 0.3138 0.4681 7 7 Vandiviere et al 1973 -1.6338 0.2270 0.0667 0.5523 8 8 TPT Madras 1980 0.0120 0.0040 0.8922 1.1481 9 9 Coetzee & Berjak 1968 -0.4717 0.0570 0.3768 1.0184 10 10 Rosenthal et al 1961 -1.4012 0.0754 0.1348 0.4276 11 11 Comstock et al 1974 -0.3408 0.0125 0.5680 0.8920 12 12 Comstock & Webster 1969 0.4466 0.5342 0.3037 10.0780 13 13 Comstock et al 1976 -0.0173 0.0716 0.5596 1.7207
Instead of the Wald-type CIs, we could choose to show these CIs in the forest plot. For consistency under this example, we may also want to use a model that directly models the $2 \times 2$ tables based on their exact likelihood under a non-central hypergeometric distribution. We can do this with:
res <- rma.glmm(measure="OR", ai=tpos, bi=tneg, ci=cpos, di=cneg, data=dat, model="CM.EL") res
Random-Effects Model (k = 13; tau^2 estimator: ML) Model Type: Conditional Model with Exact Likelihood tau^2 (estimated amount of total heterogeneity): 0.3116 (SE = 0.1612) tau (square root of estimated tau^2 value): 0.5582 I^2 (total heterogeneity / total variability): 91.4646% H^2 (total variability / sampling variability): 11.7159 Tests for Heterogeneity: Wld(df = 12) = 268.4283, p-val < .0001 LRT(df = 12) = 176.8738, p-val < .0001 Model Results: estimate se zval pval ci.lb ci.ub -0.7538 0.1801 -4.1860 <.0001 -1.1068 -0.4009 *** --- Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Now, we create the forest plot passing the log odds ratios and the log-transformed exact CI bounds to the forest() function and then use atransf=exp again for the axis transformation.1) A bit of space is added at the bottom where the pooled estimate based on the model above is added using addpoly().
with(dat, forest(yi, ci.lb=log(ci.lb), ci.ub=log(ci.ub), header=TRUE, atransf=exp, xlim=c(-8,6), at=log(c(0.05, 0.25, 1, 4, 16)), psize=1, ylim=c(-1.5, res$k+3))) abline(h=0) addpoly(res, row=-1)
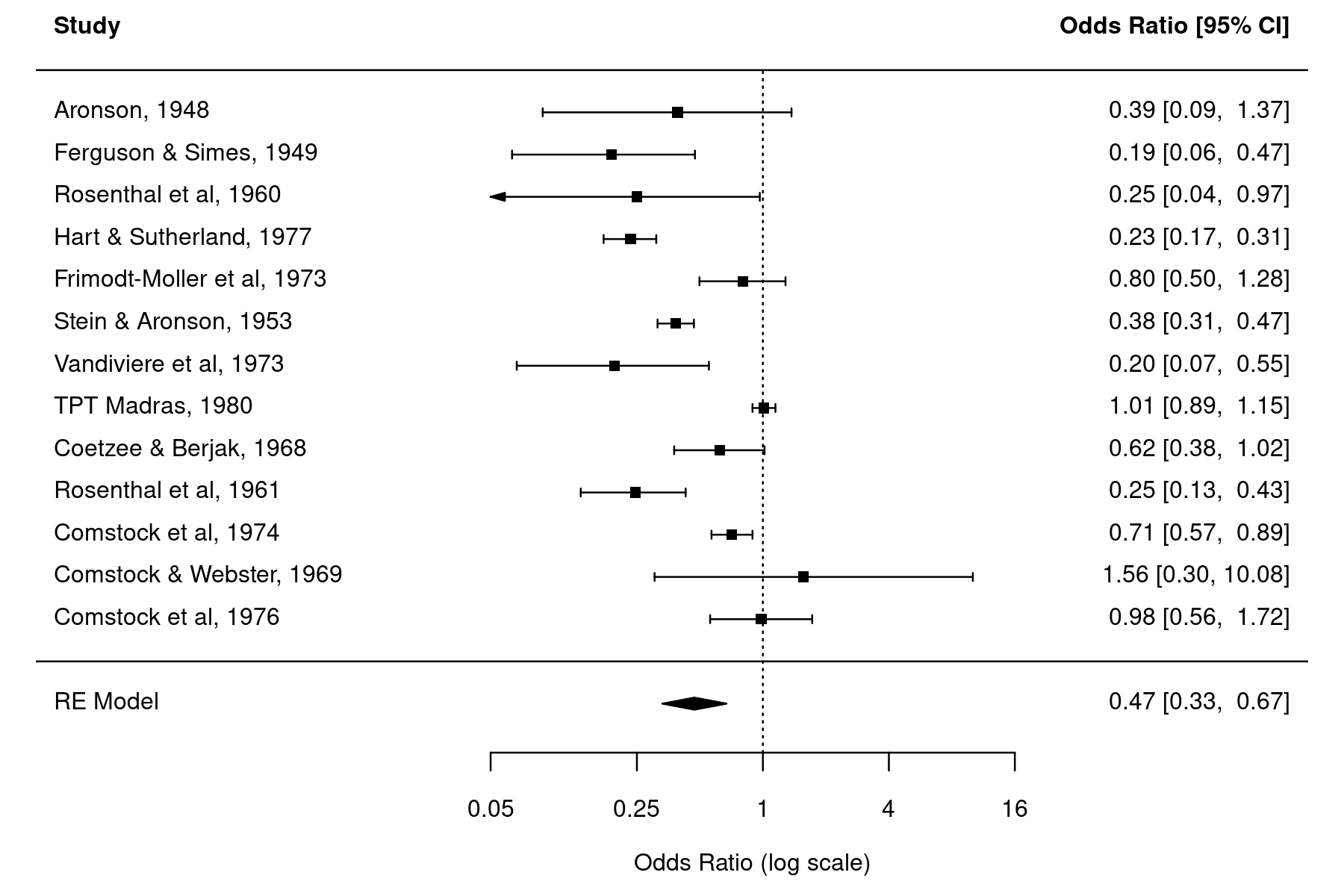
A comparison of the two forest plots shows that the latter has wider CI bounds for the individual studies, although the differences are rather negligible in most cases.2) We see somewhat more pronounced differences for smaller studies (and especially when the number of cases in the treatment and control groups are small), in which case the approximation underlying the Wald-type CI is less accurate.
The same principle as illustrated above could be used to show exact CIs for other outcome measures. However, the purpose of the forest plot is usually not to provide exact inferences about the results of the individual studies. For visualization of the individual studies and differences in their precision (as reflected in the different CI widths), using the approximate Wald-type CIs in the forest plot is often quite sufficient.