In some situations, we may want to model the association between the observed effect sizes / outcomes and some continuous moderator/predictor of interest in a more flexible manner than simply assuming a linear relationship. Below, I illustrate the use of polynomial and spline models for this purpose.
A data frame containing the data for this example can be created with:
dat <- structure(list(yi = c(0.99, 0.54, -0.01, 1.29, 0.66, -0.12, 1.18, -0.23, 0.03, 0.73, 1.27, 0.38, -0.19, 0.01, 0.31, 1.41, 1.32, 1.22, 1.24, -0.05, 1.17, -0.17, 1.29, -0.07, 0.04, 1.03, -0.16, 1.25, 0.27, 0.27, 0.07, 0.02, 0.7, 1.64, 1.66, 1.4, 0.76, 0.8, 1.91, 1.27, 0.62, -0.29, 0.17, 1.05, -0.34, -0.21, 1.24, 0.2, 0.07, 0.21, 0.95, 1.71, -0.11, 0.17, 0.24, 0.78, 1.04, 0.2, 0.93, 1, 0.77, 0.47, 1.04, 0.22, 1.42, 1.24, 0.15, -0.53, 0.73, 0.98, 1.43, 0.35, 0.64, -0.09, 1.06, 0.36, 0.65, 1.05, 0.97, 1.28), vi = c(0.018, 0.042, 0.031, 0.022, 0.016, 0.013, 0.066, 0.043, 0.092, 0.009, 0.018, 0.034, 0.005, 0.005, 0.015, 0.155, 0.004, 0.124, 0.048, 0.006, 0.134, 0.022, 0.004, 0.043, 0.071, 0.01, 0.006, 0.128, 0.1, 0.156, 0.058, 0.044, 0.098, 0.154, 0.117, 0.013, 0.055, 0.034, 0.152, 0.022, 0.134, 0.038, 0.119, 0.145, 0.037, 0.123, 0.124, 0.081, 0.005, 0.026, 0.018, 0.039, 0.062, 0.012, 0.132, 0.02, 0.138, 0.065, 0.005, 0.013, 0.101, 0.051, 0.011, 0.018, 0.012, 0.059, 0.111, 0.073, 0.047, 0.01, 0.007, 0.055, 0.019, 0.104, 0.056, 0.006, 0.094, 0.009, 0.008, 0.02 ), xi = c(9.4, 6.3, 1.9, 14.5, 8.4, 1.8, 11.3, 4.8, 0.7, 8.5, 15, 11.5, 4.5, 4.3, 4.3, 14.7, 11.4, 13.4, 11.5, 0.1, 12.3, 1.6, 14.6, 5.4, 2.8, 8.5, 2.9, 10.1, 0.2, 6.1, 4, 5.1, 12.4, 10.1, 13.3, 12.4, 7.6, 12.6, 12, 15.5, 4.9, 0.2, 6.4, 9.4, 1.7, 0.5, 8.4, 0.3, 4.3, 1.7, 15.2, 13.5, 6.4, 3.8, 8.2, 11.3, 11.9, 7.1, 9, 9.9, 7.8, 5.5, 9.9, 2.6, 15.5, 15.3, 0.2, 3.2, 10.1, 15, 10.3, 0, 8.8, 3.6, 15, 6.1, 3.4, 10.2, 10.1, 13.7)), class = "data.frame", row.names = c(NA, -80L))
We can inspect the first 10 rows of this dataset with:
head(dat, 10)
yi vi xi 1 0.99 0.018 9.4 2 0.54 0.042 6.3 3 -0.01 0.031 1.9 4 1.29 0.022 14.5 5 0.66 0.016 8.4 6 -0.12 0.013 1.8 7 1.18 0.066 11.3 8 -0.23 0.043 4.8 9 0.03 0.092 0.7 10 0.73 0.009 8.5
Variable yi contains the observed outcomes, vi the corresponding sampling variances, and xi is the predictor of interest.
Let's examine a scatterplot of these data, with the observed outcome on the y-axis, the predictor on the x-axis, and the point sizes drawn proportional to the inverse of the standard errors (such that more precise estimates are reflected by larger points).
plot(dat$xi, dat$yi, pch=21, col="black", bg="darkgray", cex=.20/sqrt(dat$vi), las=1, bty="l", xlab="Predictor", ylab="Observed Outcome", main="Scatterplot")
There is clearly an increasing relationship between the observed outcomes and the values of the predictor.
We will start by fitting a linear meta-regression model to these data. After loading the metafor package, we can do so with:
library(metafor) res.lin <- rma(yi, vi, mods = ~ xi, data=dat) res.lin
Mixed-Effects Model (k = 80; tau^2 estimator: REML)
tau^2 (estimated amount of residual heterogeneity): 0.0513 (SE = 0.0133)
tau (square root of estimated tau^2 value): 0.2264
I^2 (residual heterogeneity / unaccounted variability): 72.92%
H^2 (unaccounted variability / sampling variability): 3.69
R^2 (amount of heterogeneity accounted for): 82.88%
Test for Residual Heterogeneity:
QE(df = 78) = 303.4429, p-val < .0001
Test of Moderators (coefficient 2):
QM(df = 1) = 224.2464, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt -0.2126 0.0655 -3.2461 0.0012 -0.3409 -0.0842 **
xi 0.1058 0.0071 14.9749 <.0001 0.0919 0.1196 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The relationship is clearly significant ($p < .0001$ for the coefficient corresponding to xi). We can visualize the linear association that is implied by this model by computing the predicted average outcome for increasing values of the predictor variable and then adding the regression line to the scatterplot. The bounds of the pointwise 95% confidence intervals for the predicted values are reflected by the gray-shaded area.
regplot(res.lin, las=1, digits=1, bty="l", psize=.20/sqrt(dat$vi), xlab="Predictor", main="Linear Model")
The association between the outcome and the predictor appears to be non-linear, with the outcome barely increasing for low values of the predictor, then a steeper slope for values around the center, which then eventually seems to flatten out at the top. We could try to approximate such a relationship with a cubic polynomial model. Using the poly() function, we can easily fit such a model as follows.
res.cub <- rma(yi, vi, mods = ~ poly(xi, degree=3, raw=TRUE), data=dat) res.cub
Mixed-Effects Model (k = 80; tau^2 estimator: REML)
tau^2 (estimated amount of residual heterogeneity): 0.0281 (SE = 0.0089)
tau (square root of estimated tau^2 value): 0.1677
I^2 (residual heterogeneity / unaccounted variability): 58.83%
H^2 (unaccounted variability / sampling variability): 2.43
R^2 (amount of heterogeneity accounted for): 90.60%
Test for Residual Heterogeneity:
QE(df = 76) = 171.5545, p-val < .0001
Test of Moderators (coefficients 2:4):
QM(df = 3) = 357.6414, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt 0.0563 0.0998 0.5644 0.5725 -0.1392 0.2518
poly(xi, degree = 3, raw = TRUE)1 -0.1431 0.0551 -2.5995 0.0093 -0.2510 -0.0352 **
poly(xi, degree = 3, raw = TRUE)2 0.0417 0.0081 5.1476 <.0001 0.0258 0.0576 ***
poly(xi, degree = 3, raw = TRUE)3 -0.0018 0.0003 -5.3850 <.0001 -0.0025 -0.0011 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
To visualize this association, we can again draw a scatterplot with the model-implied regression line.
xs <- seq(-1, 16, length=500) sav <- predict(res.cub, newmods=unname(poly(xs, degree=3, raw=TRUE))) regplot(res.cub, mod=2, pred=sav, xvals=xs, las=1, digits=1, bty="l", psize=.20/sqrt(dat$vi), xlab="Predictor", main="Cubic Polynomial Model")
The model does appear to capture the non-linearity in the association. However, a general problem with polynomial models of this type is that they often suggest nonsensical patterns for very low or very high values of the predictor. In this case, the model suggests an initial decrease at the low end and a drop at the high end, which might not be realistic.
As an alternative approach, we could consider fitting a spline model. One popular model of this type consists of a series of piecewise cubic polynomials (Stone & Koo, 1985). Such a 'restricted cubic spline' model can be easily fitted with the help of the rms package. For this, we need to choose the number of 'knots', which are the positions where the piecewise cubic polynomials are connected. Here, I choose 4 knots, which yields a model with the same number of parameters as the cubic polynomial model we fitted above.
library(rms) res.rcs <- rma(yi, vi, mods = ~ rcs(xi, 4), data=dat) res.rcs
Mixed-Effects Model (k = 80; tau^2 estimator: REML)
tau^2 (estimated amount of residual heterogeneity): 0.0262 (SE = 0.0085)
tau (square root of estimated tau^2 value): 0.1619
I^2 (residual heterogeneity / unaccounted variability): 57.08%
H^2 (unaccounted variability / sampling variability): 2.33
R^2 (amount of heterogeneity accounted for): 91.24%
Test for Residual Heterogeneity:
QE(df = 76) = 165.4692, p-val < .0001
Test of Moderators (coefficients 2:4):
QM(df = 3) = 374.5340, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt 0.0070 0.0902 0.0773 0.9384 -0.1698 0.1838
rcs(xi, 4)xi -0.0242 0.0315 -0.7693 0.4417 -0.0859 0.0375
rcs(xi, 4)xi' 0.4506 0.0870 5.1777 <.0001 0.2801 0.6212 ***
rcs(xi, 4)xi'' -1.4035 0.2537 -5.5326 <.0001 -1.9007 -0.9063 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
To compute predicted values based on this model, we first need to determine the knot positions as chosen by the rcs() function.1)
knots <- attr(rcs(dat$xi, 4), "parms") knots
[1] 0.200 5.295 10.100 15.000
We can then use the rcspline.eval() function with these knot positions to compute predicted values, which we can add to the scatterplot. The knot positions are also shown in the figure as dotted vertical lines.
sav <- predict(res.rcs, newmods=rcspline.eval(xs, knots, inclx=TRUE)) tmp <- regplot(res.rcs, mod=2, pred=sav, xvals=xs, las=1, digits=1, bty="l", psize=.20/sqrt(dat$vi), xlab="Predictor", main="Restricted Cubic Spline Model") abline(v=knots, lty="dotted") points(tmp)
The model now suggests that the association flattens out at the lower and upper tails.
For further details on restricted cubic spline models, see Harrell (2015). The book covers their use in the context of 'standard' regression analyses, not meta-regression, but the information provided there (e.g., on choosing the number of knots and the knot locations) is equally applicable in the present context.
The splines package (which is one of the 'base' packages that comes with R) can also be used to fit such spline models (which are also called natural cubic splines) using the ns() function. Note that this function makes a distinction between the 'inner' knots and the 'boundary' knots. So, if we want to obtain the same results as above using rcs(), we should use the following code.
library(splines) ns.knots <- knots[2:3] ns.Boundary.knots <- knots[c(1,4)] res.ns <- rma(yi, vi, mods = ~ ns(xi, knots=ns.knots, Boundary.knots=ns.Boundary.knots), data=dat) res.ns sav <- predict(res.ns, newmods=unname(ns(xs, knots=ns.knots, Boundary.knots=ns.Boundary.knots))) tmp <- regplot(res.lin, pred=sav, xvals=xs, las=1, digits=1, bty="l", shade="gray80", psize=.20/sqrt(dat$vi), xlab="Predictor", main="Natural Cubic Spline Model") abline(v=ns.knots, lty="dotted") abline(v=ns.Boundary.knots, lty="dotted") points(tmp)
Also note that the ns() function constructs the spline terms in a different parameterization as rcs() so the model coefficients will differ when comparing the output from the two models. However, the fit of the model is identical (as can be confirmed with fitstats(res.rcs, res.ns)) and hence the corresponding figure is not shown, as it would be identical to the one we obtained above using rcs().
As an alternative, we can consider a so-called thin plate spline model to examine the relationship between the outcome and predictor. The mgcv package provides the necessary functionality for this.
library(mgcv)
First, we use the smoothCon() function to transform the original predictor variable into a set of new predictor variables. Here, k is set to 4, which results in a model with the same degree of complexity as we have considered above.
sm <- smoothCon(s(xi, bs="tp", k=4), data=dat, absorb.cons=TRUE)[[1]]
Then we can use this model matrix in our meta-regression model:2)
res.tps <- rma(yi, vi, mods = ~ sm$X, data=dat) res.tps
Mixed-Effects Model (k = 80; tau^2 estimator: REML)
tau^2 (estimated amount of residual heterogeneity): 0.0265 (SE = 0.0086)
tau (square root of estimated tau^2 value): 0.1628
I^2 (residual heterogeneity / unaccounted variability): 57.36%
H^2 (unaccounted variability / sampling variability): 2.35
R^2 (amount of heterogeneity accounted for): 91.14%
Test for Residual Heterogeneity:
QE(df = 76) = 166.0947, p-val < .0001
Test of Moderators (coefficients 2:4):
QM(df = 3) = 371.6700, p-val < .0001
Model Results:
estimate se zval pval ci.lb ci.ub
intrcpt 0.6247 0.0272 22.9620 <.0001 0.5713 0.6780 ***
sm$X1 0.7319 0.1295 5.6506 <.0001 0.4780 0.9858 ***
sm$X2 0.0290 0.1084 0.2675 0.7891 -0.1835 0.2415
sm$X3 -0.1572 0.1219 -1.2898 0.1971 -0.3962 0.0817
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
As above, we can visualize these results by superimposing the regression line (with a 95% confidence interval band) on top of the scatterplot.
sav <- predict(res.tps, newmods=PredictMat(sm, data.frame(xi=xs))) regplot(res.lin, mod=2, pred=sav, xvals=xs, las=1, digits=1, bty="l", psize=.20/sqrt(dat$vi), xlab="Predictor", main="Thin Plate Spline Model")
Again, we see that that the model suggests a flattening of the curve at the tails.
For further details on thin plate splines, see Wood (2017).
We can compare the models in terms of their log likelihoods and information criteria:
fitstats(res.lin, res.cub, res.rcs, res.tps)
res.lin res.cub res.rcs res.tps logLik: -19.25878 -7.965164 -7.141379 -7.321693 deviance: 38.51756 15.930328 14.282757 14.643387 AIC: 44.51756 25.930328 24.282757 24.643387 BIC: 51.58769 37.583995 35.936424 36.297053 AICc: 44.84188 26.787471 25.139900 25.500530
Clearly, the models that allow for a non-linear relationship provide a better fit (i.e., have higher log likelihood values) and strike a better balance between this increased fit and the increased model complexity (as indicated by the lower values of the information criteria). On the other hand, differences between the cubic polynomial, restricted cubic spline, and thin plate spline models are relatively minor in comparison, with a slight advantage for the latter two models.
We can visualize all models in the same figure as follows:
cols <- c("black", "dodgerblue", "firebrick", "forestgreen") regplot(res.lin, las=1, digits=1, bty="l", ci=FALSE, lcol=cols[1], lwd=5, psize=.20/sqrt(dat$vi), xlab="Predictor", main="Model Comparison") sav <- predict(res.cub, newmods=unname(poly(xs, degree=3, raw=TRUE))) lines(xs, sav$pred, lwd=5, col=cols[2]) sav <- predict(res.rcs, newmods=rcspline.eval(xs, knots, inclx=TRUE)) lines(xs, sav$pred, lwd=5, col=cols[3]) sav <- predict(res.tps, newmods=PredictMat(sm, data.frame(xi=xs))) lines(xs, sav$pred, lwd=5, col=cols[4]) legend("topleft", inset=.02, lty="solid", col=cols, lwd=5, legend=c("Linear Model", "Cubic Polynomial", "Restricted Cubic Spline Model", "Thin Plate Spline Model"))
The figure shows that the two spline models yield essentially the same fit.
Harrell, F. E., Jr. (2015). Regression modeling strategies: With applications to linear models, logistic and ordinal regression, and survival analysis (2nd ed.). New York: Springer.
Stone, C. J., & Koo, C.-K. (1985). Additive splines in statistics. In Proceedings of the Statistical Computing Section ASA. Washington, DC: American Statistical Association.
Wood, S. N. (2017). Generalized additive models: An introduction with R (2nd ed.). Boca Raton, FL: CRC Press.
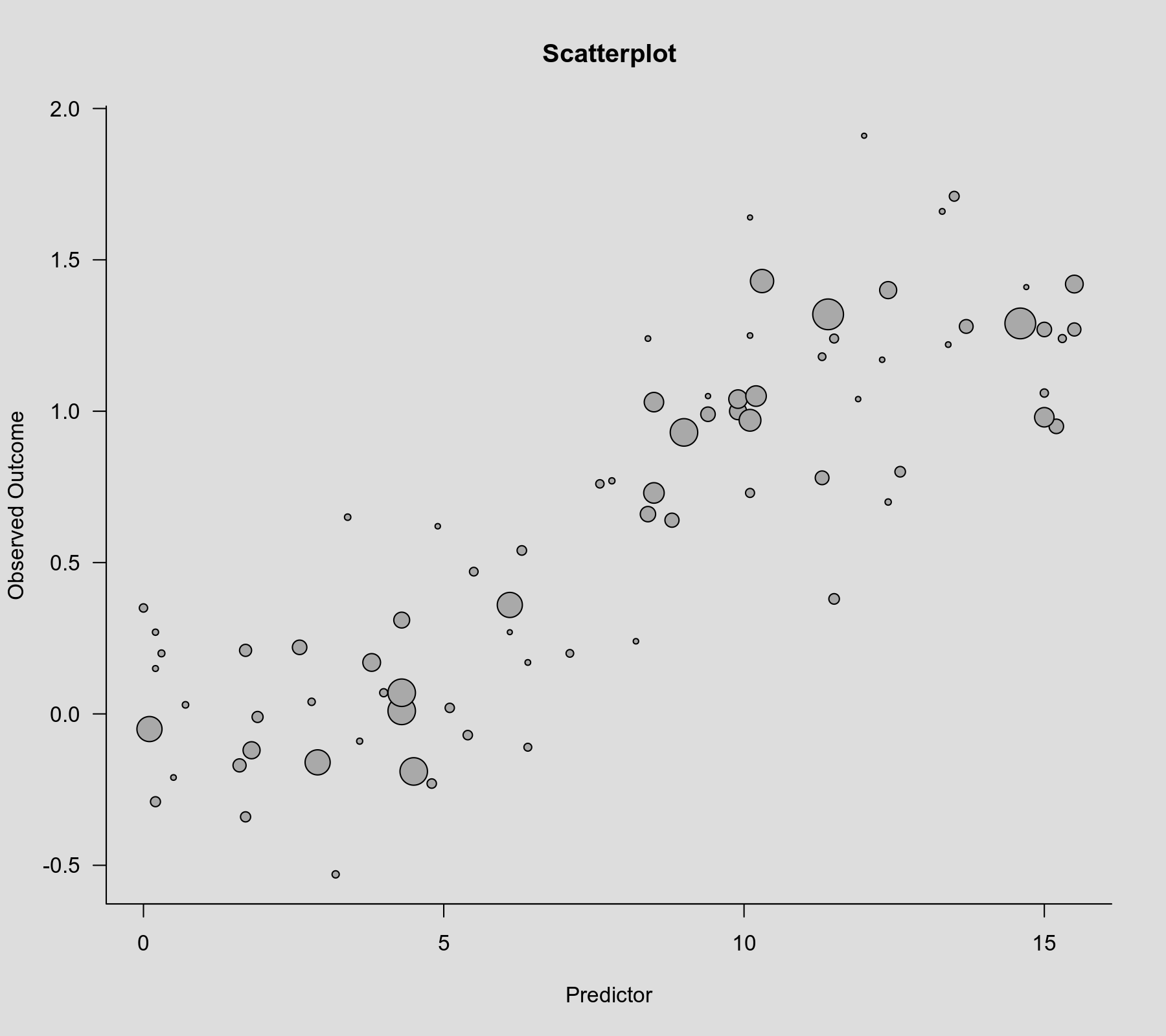
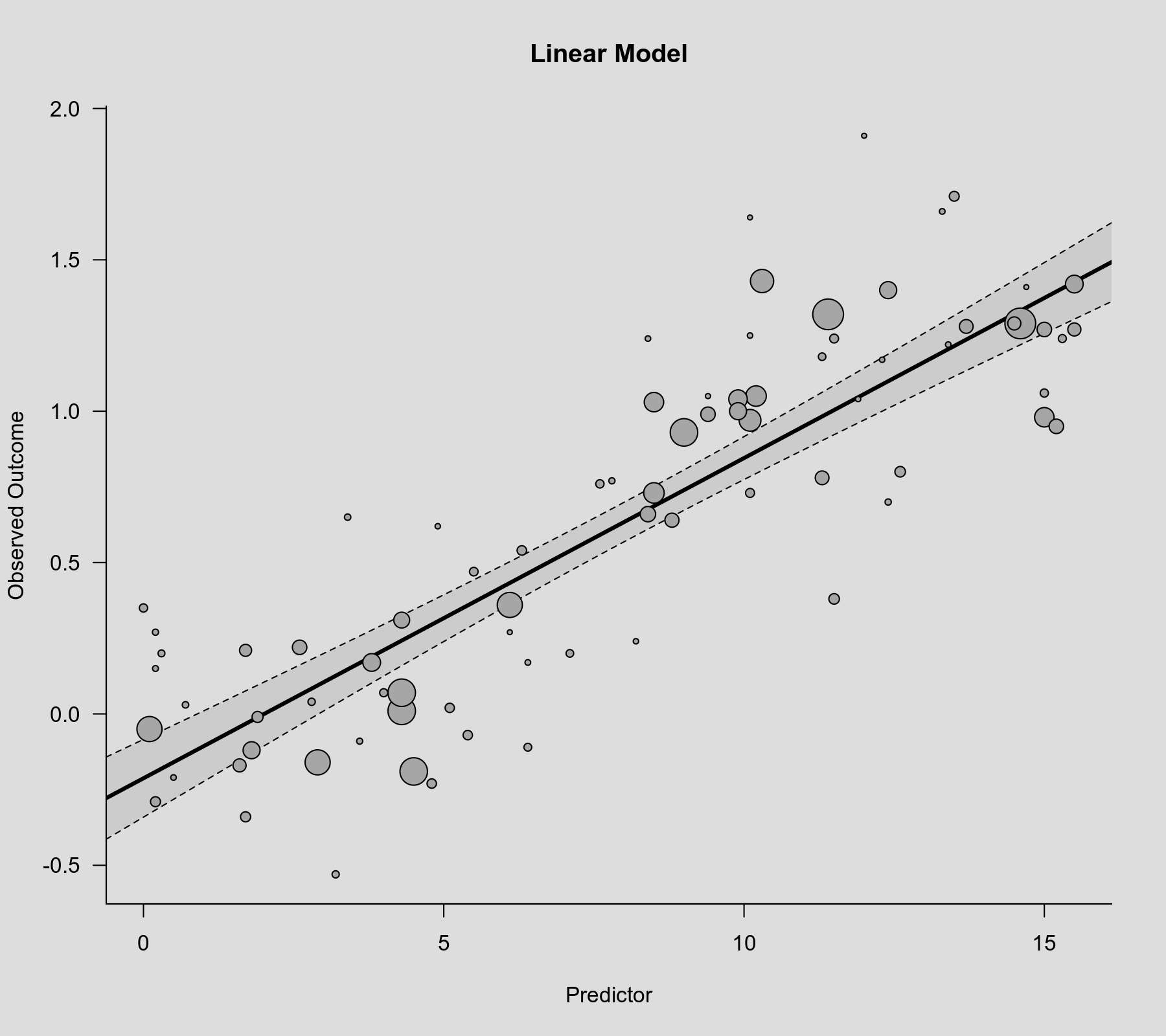
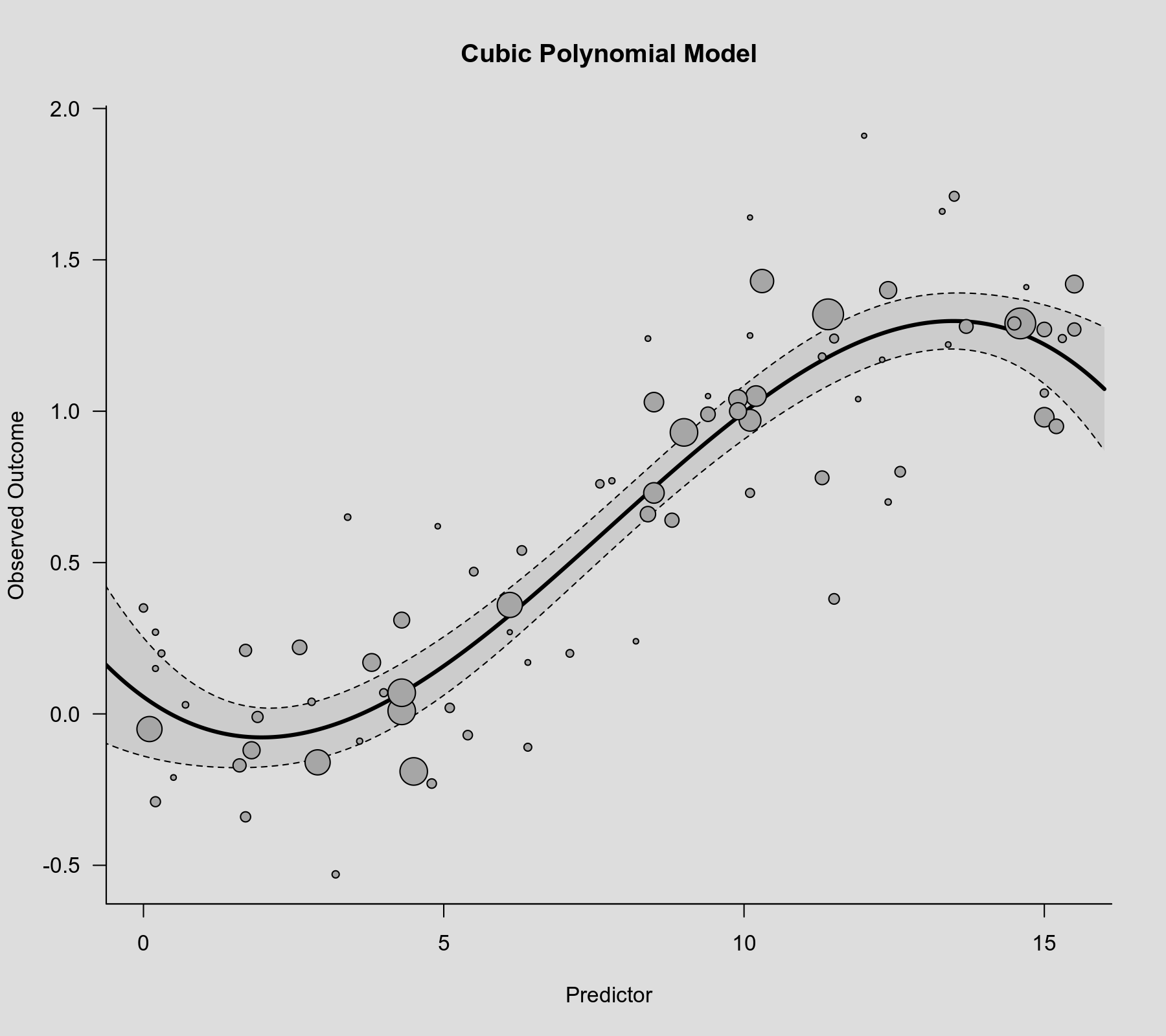
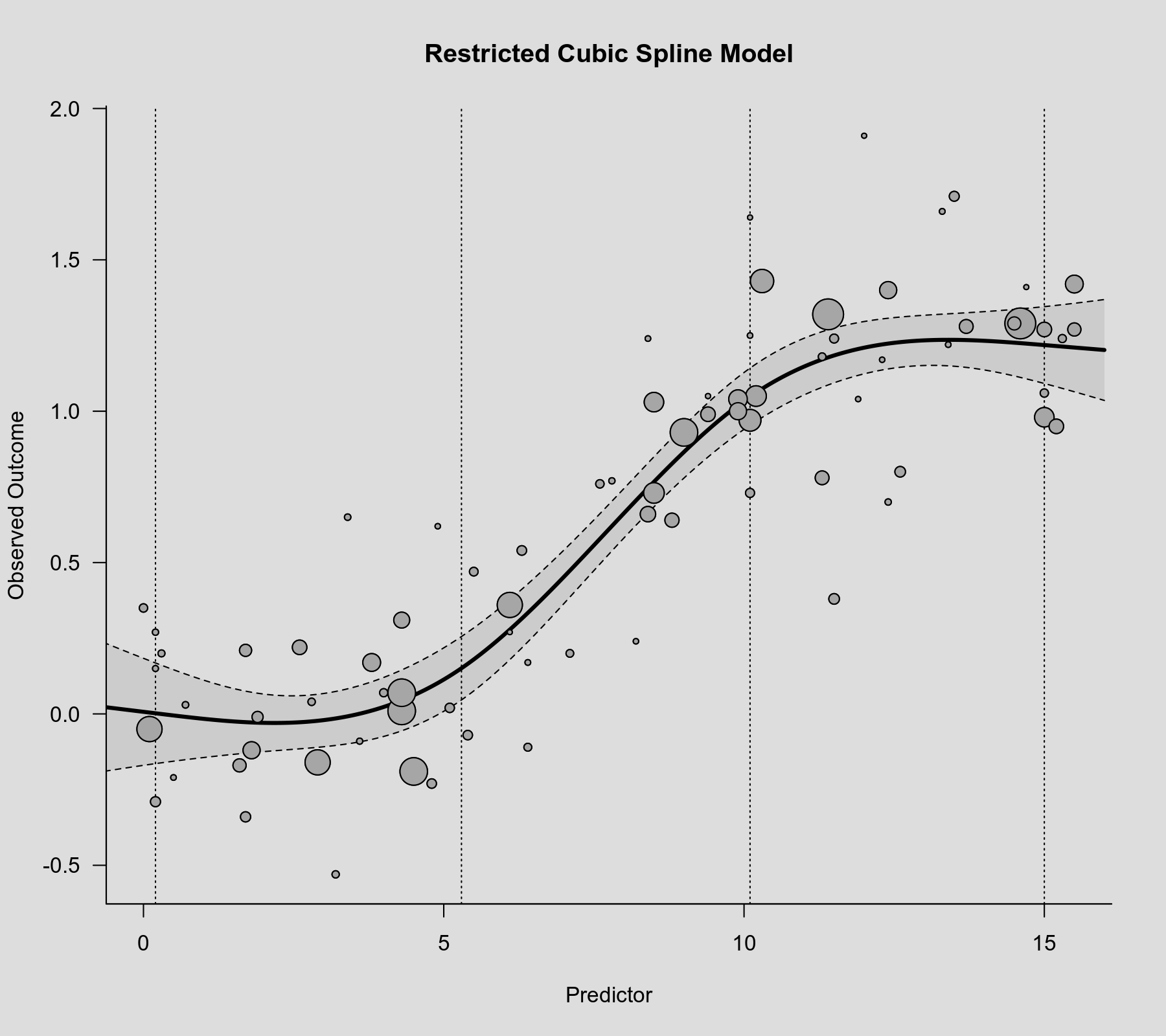
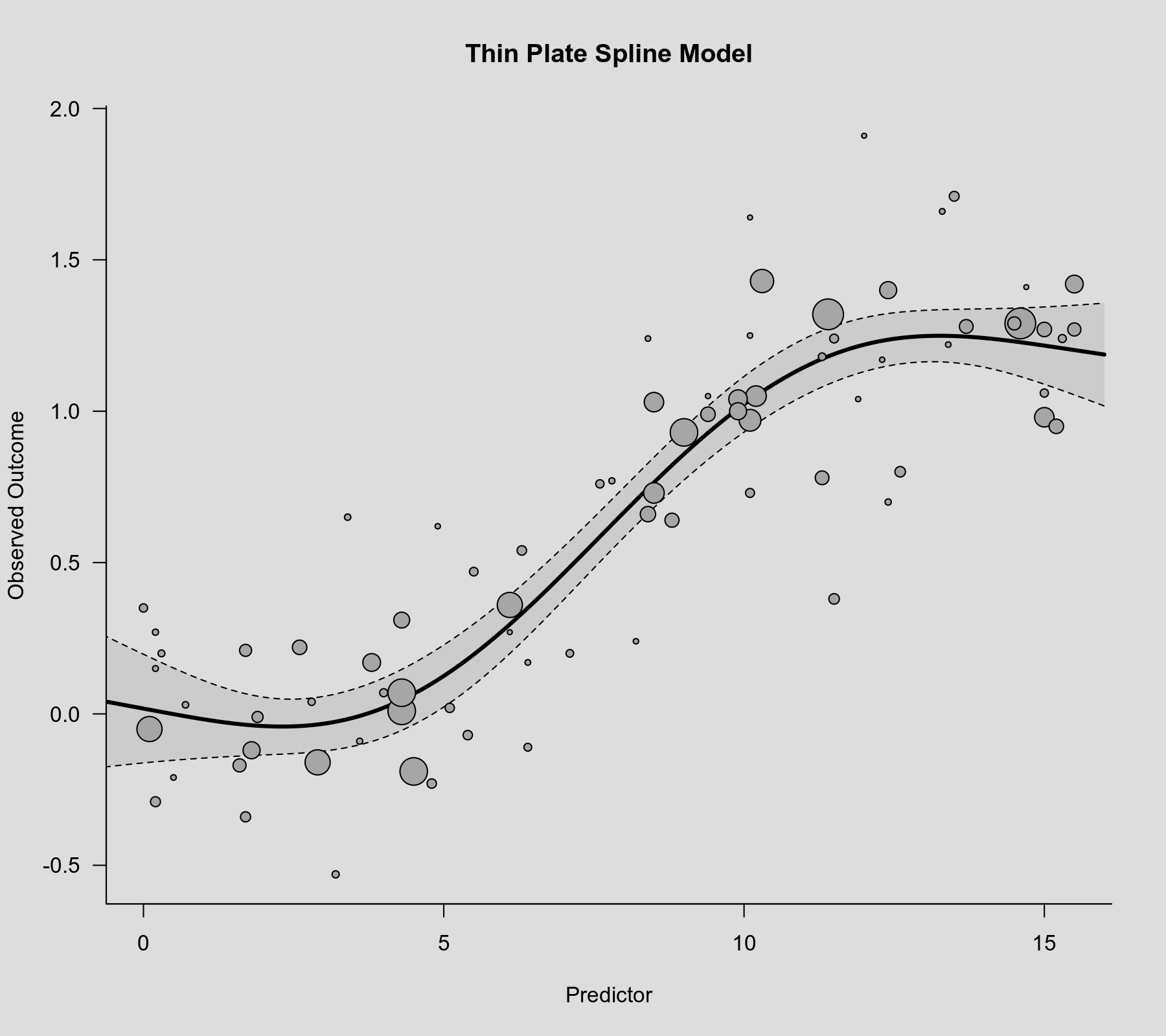
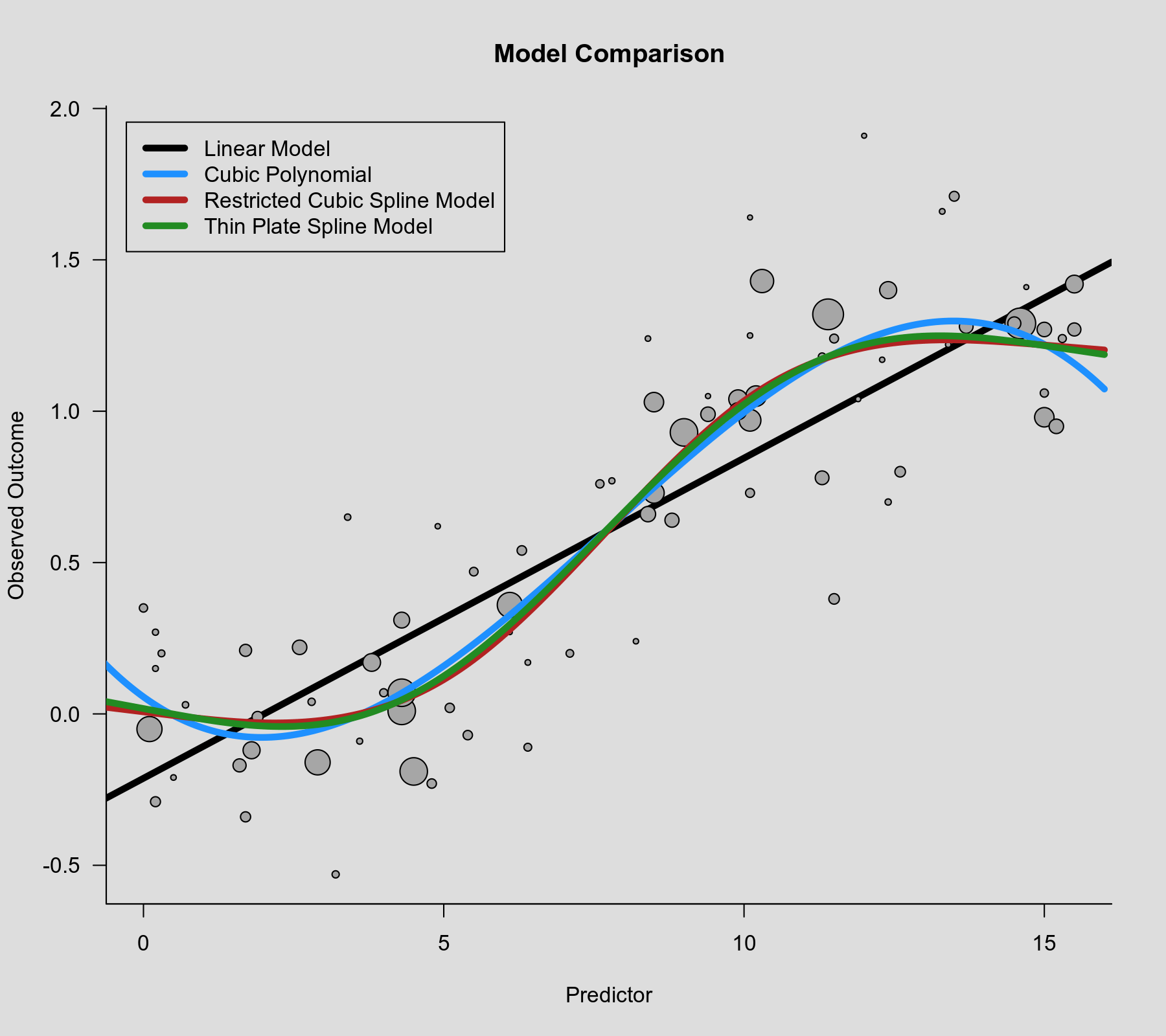
rcs() function as the second argument. Also note that rcs(xi, 4) will select the knot positions based on all (non-missing) xi values, but if there are (additional) missing values in yi and/or vi, then the actual analysis will be based on a subset of the data for which the chosen knot positions might not be ideal.